波がたつ、波をうつ

前回の」ポスト＜時間の方向＞で波の現象に関連して時間表現の後（うしろ）と前（まえ）の話をしたが、今回は波関連の日本語表現をチェックしてみる。

波がたつ

＜波がたつ＞は＜波が立つ＞でいいだろう。これは波、特に水面上の波をよく観察した表現だ。水面上の波は前後、左右に進んでるようにみえる（こともある）がよく見ると水面がその場で上下運動しているだけなので＜波が立つ＞でいい。上下運動を強調すると＜波が立ったりすわったり＞になるか？もっと一般的には

波がおこる
波が出る

波がなくなる、消える
波がおさまる、静（しず）まる

は問題ない。波を風で置き換えられるので波も風も同じような自然現象ととらえていたのだろう。


波が寄せる
波が寄せて来る

という言い方はあるが

波が寄せて行く

は変だ。波は動いて行く、進んで行くように見えるが上記のように＜よく見ると水面がその場で上下運動しているだけなので＞

波が動いて行く、
波が進んで行く

というのもあまり聞かない。

＜流れる＞はまったくダメで

波が流れる
波が流れて来る
波が流れて行く

したがって波は＜流れる＞ものではないのだ。

波は間違いなく動いているが、＜波が流れる＞と同じく

波が動く

は聞かない。

 
波をうつ

＜波をうつ ＞は＜波を打つ＞ではしっくりこない。 ＜波がうつ ＞ではなく文法違反のような＜波をうつ ＞で

水面が波をうつ 。
表面が波をうつ。

という言い方なので＜波をうつ ＞で＜波のような状態をしている ＞という意味になる。

水面が波うつ 。
表面が波うつ。

も自然な表現だ。

波打ち際（ぎわ）

という言い方があるが、これは＜波が打ちつける、寄せて来る際（きわ）、端 （はし）、ところ＞で＜波うつ＞とは違う。

ほかの＜ｘｘをうつ＞表現をさがしてみると

脈をうつ（脈うつ）
あいづちをうつ　－　あいづちは相槌か。＜鎚（つち）を打つ＞ も少し変で＜ｘｘを鎚で打つ＞が実情に合っている。したがって＜あいづち＞は波、脈のような反復運動と見た言い方だ。


波にのる　－　これは波に乗って前に進むような感じがある。これは比喩的に使われる。

波に逆（さか）らう　－　これは押し寄せてくる波に逆らう。または波の上下運動に逆らう。これも多くは比喩的に使われる。

波風（なみかぜ）をたてる　－　風が吹いて波が立つ、が実情でこれを比喩的に＜風を吹かして波を立てる＞の意か。あるいは＜波や風をたてる＞の意か。だが＜風をたてる＞はほとんど聞かないが＜風立ちぬ＞という詩だか小説がある。


波がゆれる

＜波にゆられて＞、＜波が船をゆらす＞はいいが＜波がゆれる＞は変だ。細かいことを言うと波がゆれないと＜波にゆられて＞や＜波が船をゆらす＞は不可能なはずだ。これは＜波は自動的に動く、自動詞＞にならないということか？だが＜波をゆらす＞もダメだ。なんだかかなりこんがらかってきた。 振動表現では＜振れる、振らす、振るわす、震える、震わす＞があるが波には使われないいうだ、


ｓｐｔｔ

時間の方向

時間の（経過の）方向表現についてはどこかで書いたような気がするが、最近＜波の方程式（Wave equations）＞に何度目かの挑戦をしているが、次のような式と解説に出くわしたので、この言葉の問題を思いだした。＜波の方程式＞あるいは＜波の現象＞を深く理解するのは難関といえるがおもしろくもある。引用が長くなるので、引用は＜時間の方向＞に関係のあるところだけにしたが、それでも長いので、末尾に引用（コピー、ペースト）した。＜次のような式と解説＞のところだけここに引用すると

”

 

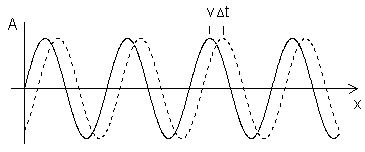
(V = velocity)

In terms of these parameters we can express a pure traveling wave as the function

A(t,x) = A0 cos(kx - ωt)

where the "amplitude" A₀ is the maximum of the function. (We use the cosine function rather than the sine merely for convenience, the difference being only a matter of phase.) The minus sign denotes the fact that if we hold t constant and increase x we are moving "to the right" along the function, whereas if we focus on a fixed spatial location and allow time to increase, we are effectively moving "to the left" along the function (or rather, it is moving to the right and we are stationary). Reversing the sign gives A₀ cos(kx + ωt), which is the equation of a wave propagating in the negative x direction. Note that the function A(t,x) is the fundamental solution of the (one-dimensional) "wave equation"

”

一番目の式は＜a pure traveling wave as the function＞。一方二番目の式は＜ "wave equation"＞で、一番目の式は二番目の式の解ということなのだが、なぜ解になるかの説明はこれまた別の話でこの引用の中にはない。いろいろあったてみたが、解が説明なしにでてくる説明が多い。解の出し方は場合によると、ＩＱが高くアイデア豊富な数学者の遊びみたいなところがある。

さて、問題の箇所は

The minus sign denotes the fact that if we hold t constant and increase x we are moving "to the right" along the function, whereas if we focus on a fixed spatial location and allow time to increase, we are effectively moving "to the left" along the function (or rather, it is moving to the right and we are stationary). 

（ｓｐｔｔ訳）

負記号は＜t を一定（つまりは時間を止める）とし x を増加させると我々はこの方程式に沿って右方向に行き、一方もし我々が空間の一点に位置を定めて（動かず）、時間を経過させる（allow time to increase）と我々は結果的に（effectively）この方程式にに沿って左方向に動くことになる（あるいはむしろ、それは右方向に動き、我々はとどまっている）。

＜波の方程式＞に慣れていないひとは、おそらく原文の英語もわたしの日本語訳も理解しずらいだろう。 こまかく見ると

x を増加させると我々はこの方程式にに沿って右方向に行き:  ＜ x を増加させる（x が増加すると）＞こと自体、矢印があるのでＡ軸の値に関係なく矢印方向、つまり右方向へ動くことだ。

もし我々が空間の一点に位置を定めて（動かず）、時間を経過させると：　これは波のある池かプールの水面に浮く落ち葉を想像するといい。場所は波があるところならどこでもいい。落ち葉は上下にほぼ規則的（ピストンのように）動くが、基本的（理想的）には前や後ろ、右や左には移動しない。そしてこの落ち葉の動きを観察することに似ている。あるいは落ち葉の身になったもいい。

この上下の運動の速度を見ると上限、下限では瞬間的に止まっている。また上限、下限に近づくほどのろく、または上限、下限から離れるにしたがってだんだん早くなる。一番早いのは上限、下限の中間点（Ａ値＝０、ｘ軸上）だ。これは三角関数で、円周を等速度で動く点を下面、または側面に投影した時の点の動きだ。
あるいは机の上に紙を置き、紙の上で鉛筆やペンで上下（または左右）に動かし、同時に紙を90度の角度で（つまりは上下運動の場合は紙を右か左の方向に、左右運動の場合は紙を上か下に）動かすときにできる軌跡はサイン（コサイン）カーブになる。

さて問題はその次で

（時間を経過させると（allow time to increase））我々は結果的に（effectively）この方程式にに沿って左方向に動くことになる。

これは理解しずらい。ここが＜負記号なので左方向に動く＞の説明なのだろうが、時間は経過しているが＜我々空間の一点に位置を定めて（動かず）＞ているのだ。矛盾するようだが、したがって（実際はそうではないが）＜結果的に（effectively）＞＜この方程式にに沿って左方向に動くことになる＞と言っているのか？

これは上のコサインカーブを使うと

我々は空間の一点に位置を定めて（動かず）、その場で観察点（落ち葉）の上下運動 、または＜我々＞が上下に動くとして上下運動の軌跡（A軸上の値）は＜左方向にグラフ＞をなぞることになる。

＜結果的に（effectively）この方程式にに沿って左方向に動くことになる＞ はこのようなことを言っているのだろう。

次のカッコ内の説明。

（あるいはむしろ、それは右方向に動き、我々はとどまっている）

この＜それ＞はなにか？　＜我々はとどまっている＞とはどういう意味か？なぜ今度は（それが）＜右方向に動く＞のか。

これはたとえば、バスに乗っていて、 乗っているバスは止まっているが隣のバスが前進すると自分のバスは後ろに動いている感じがある（錯覚）。この類か？（バスは大きいので、接近している隣のバスの一部しか見えず、背景はもちろん上下も見えない）。上のグラフの点線グラフが＜それ＞か？

おもしろいのは＜allow time to increase＞で文字通りには＜時間を増やす＞の意だが＜時間を経過させる＞ことだろう。

初めのグラフは時間を止めたときの波を横からみたものだが、場所を固定して（if we focus on a fixed spatial location and allow time to increase）＜時間を経過させる＞場合のグラフも上述のようにサイン（コサイン）カーブになる。グラフにした場合x軸が時間軸（t 軸）になる。問題は矢印の方向だ。時間は目に見えず、視覚化することは難しい。20年ほど前（2000年ごろ）に中国の会社から送られきた技術文書で時間軸（矢印の）方向が右から左になっているグラフをもらったことがある。＜おかしい＞と返事をしたら訂正してきた。

オシロスコープ （Wiki）

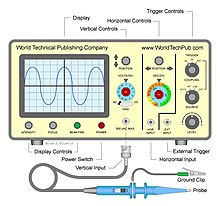
 オシロスコープに出てくる波形は時間の経過とともに右へ動いていく（ように見える）。サイン、コサインカーブだとわかりにくいが不規則な山谷グラフでは左から右への移動がよくわかる。たいていは常に動いているが、時間を止めたとして、あるいは写真をとったとすると、x= 0が現在で右側は過去の値を時間軸上に示していることになる。それではx= 0、現在(多分）の左側はなにか？奇妙といえば奇妙で、右端を現在としてその左側を過去の値を＜逆の方向の時間軸＞で示すようすれば、左端が一番古い値となる。過去の値は古い順に左端から消えていく。このほうが＜理＞にかなっている。または＜直観＞を裏切らない。だがオシロスコープが示すものは時間的に＜前＞の値が位置上、視覚上（感覚的に）＜前＞にあるわけで統一がとれているともいえる。無意識だが人の目は左から右へスキャンしてものを見ている。
  ＜川の流れは絶えずして . . . . .＞というのがあるが、これだと過去（の川の水、あるいは水に浮かぶ木の葉）は前に進み見えなくなる（消えていく）のでこのオシロスコープの動きと同じになる。

＜時間はどんどん去って行く＞という場合＜前に去って行くのか＞、はたまた＜後ろへ去って行く＞のか。これは後ろも前もないだろう。時間軸の方向（矢印）はかなり恣意的だ。

では＜過去の出来事はどんどん去って行く＞という場合＜前に去って行くのか＞、はたまた＜後ろへ去って行く＞のか？

波のやっかいなところは、上で見たように、波形は時間の経過とともにある方向へ動いていくように見えるが、よく見ると実際はその場で高さが上下しているだけなことだ。だがこれまた実際はそう簡単ではない。上下運動とは別にある方向へ動いているように見えるのも確かのようだが錯覚か？

一方波形以外の普通のグラフではx軸を時間軸と見た場合、たとえば (from Wiki)

  

y=-2x+4

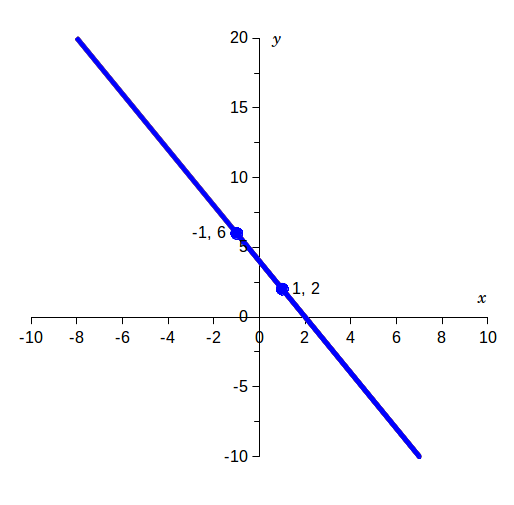
で、x = 1, 2, 3 . . . . . を1秒、2秒、3秒. . . . .  とすると、x=0 が現在で y= 4, 1秒後には y= 2 になり, 1秒前は y=6 だったとみるのが普通ではないか？

この＜後、前＞という言い方は間違いではない。これまた奇妙といえば奇妙だ。

このグラフの式y=-2x+4 の＜+4＞を+3、+2、+1、0、－1、－2、－3 に替えるとグラフは下へ下がっていくが（y軸のー方向）、同時にグラフはそのまま左側に移動する。

逆にy=-2x+4 の＜+4＞を+5、+6、+に替えるとグラフは上に上がっていくが（y軸の＋方向）、同時にグラフは右側にこれまたそのまま移動する。



末尾

おもしろい問題なので重複するところもあるが解説を続ける。言葉の問題についてのコメントはあまりないので、興味とヒマのある人だけ読み続けてください。（他のブログに移す予定）
 
https://www.mathpages.com/home/kmath210/kmath210.htm

"

Phase, Group, and Signal Velocity

The velocity of a wave can be defined in many different ways, partly because there many different kinds of waves, and partly because we can focus on different aspects or components of any given wave. The ambiguity in the definition of "wave velocity" often leads to confusion, and we frequently read stories about experiments purporting to demonstrate "superluminal" propagation of electromagnetic waves (for example). Invariably, after looking into the details of these experiments, we find the claims of "superluminal communication" are simply due to a failure to recognize the differences between phase, group, and signal velocities.

"

Note (sptt)

to purport: appear to be or do something, especially falsely.

superluminal :  Faster-than-light (also superluminal or FTL) communications and travel are the conjectural propagation of information or matter faster than the speed of light. The special theory of relativity implies that only particles with zero rest mass may travel at the speed of light. (Wiki)

これは＜Group, and Signal Velocity＞に関連していることのようで、この引用には詳しい説明はない。この引用はPhase Velocity 関連だけだ。

"  

In the simple case of a pure traveling sinusoidal wave we can imagine a "rigid" profile being physically moved in the positive x direction with speed v as illustrated below.

(V = Velocity)

Clearly the wave function depends on both time and position. At any fixed instant of time, the function varies sinusoidally along the x axis, whereas at any fixed location on the x axis the function varies sinusoidally with time. One complete cycle of the wave can be associated with an "angular" displacement of 2π radians. The angular frequency ω of a wave is the number of radians per unit time at a fixed position, whereas the wave number k is the number of radians per unit distance at a fixed time. (If we prefer to speak in terms of cycles rather than radians, we can use the wavelength λ = 2π/k and the frequency ν = ω/2π.)

"

The angular frequency ω of a wave is the number of radians per unit time at a fixed position とあるが

1 radian はradius / 2πr、すなわち1 / 2π のことなのでここは

ω: angular frequency. the number of 2π radians (1 cycle)  per unit time at a fixed position

日本語では角周波数はあまり聞かないが、角速度 angular velocity が距離 / 時間にたいし、回転数 / 時間のことで、１回転（360度）が2π radians になる。つまりは単位時間あたりに（１秒間に）何回転するかだ。ω = 2πf （f = frequency) なので ω は2π radians=１回転が1秒間に何回あるか、というこだ。1ω = １回転/秒。10ω = 10回転/秒。単位はラジアン/秒だが、実際はthe nukber of 2π radians / sec のことになる。コンセプトの問題で繰り返しになるが、ω = 2πf （f = frequency) なので、ω は周波数に2π（ラジアン）を掛けたもの。

＜at a fixed position＞refers to ＜any fixed location on the x axis the function varies sinusoidally with time.＞  

この箇所は

もし我々が空間の一点に位置を定めて（動かず）、時間を経過させると：　これは波のある水面に浮く落ち葉を想像するといい。場所は波があるところならどこでもいい。落ち葉は上下にほぼ規則的（ピストンのように）動くが、基本的（理想的）には前や後ろ、右や左には移動しない。そしてこの落ち葉の動きを観察することに似ている。あるいは落ち葉の身になったもいい。

この上下の運動の速度を見ると上限、下限では瞬間的にとまっている。また上限、下限に近づくほどのろく、または上限、下限から離れるにしたがってだんだん早くなる。一番早いのは上限、下限の中間点（Ａ値＝０、ｘ軸上）だ。これは三角関数で、円周を等速度で動く点を下面、または側面に投影した時の点の動きだ。

あるいは机の上に紙を置き、紙の上で鉛筆やペンで上下（または左右）に動かし、同時に紙を90度の角度で（つまりは上下運動の場合は紙を右か左の方向に、左右運動の場合は紙を上か下に）動かすときにできる軌跡はサイン（コサイン）カーブになる。

に相当する。 

whereas the wave number k is the number of radians per unit distance at a fixed time. (If we prefer to speak in terms of cycles rather than radians, we can use the wavelength λ = 2π/k and the frequency ν = ω/2π.)

 
the frequency ν = ω/2π.

 ν はvではなく、ギリシャ文字で、普通はf（frequency） を’つかう。一方＜k＞の方はいくつか違った定義があるようようだが、ここでは

λ = 2π/k

入れ替えると

 　　　　2π　

k　＝　－－

　　　　　λ

という定義だ。 これはわかりずらいが

k is the number of radians （2π radians （1 cycle)) per unit distance at a fixed time に対応することになる。時間は止まっており（a fixed time）per unit distance （1 meter）あたり（2π radians （1 cycle) の距離（＝波長）がいくつあるかということなのだが、上の式では2π が明示されており、なんだかよくわからなくなっている。2π は距離ではない。1m　を超える波長もあるが、たいていは波長もっと短い。したがって1m の中に何度も1波長がとれ、そのとれる回数をいっているのだ。上の式はこれにさらに2π をかけているのだが、これは

ω = 2πf （f = frequency)　－　単位ラジアン

に対応させたもので 

  　　　　　　　1　

k　＝　2π　－－　　－　単位ラジアン

　　　　　　　　λ

としている。

”
In terms of these parameters we can express a pure traveling wave as the function

A(t,x) = A₀ cos(kx - ωt)

where the "amplitude" A₀ is the maximum of the function. (We use the cosine function rather than the sine merely for convenience, the difference being only a matter of phase.) The minus sign denotes the fact that if we hold t constant and increase x we are moving
 "to the right" along the function, whereas if we focus on a fixed spatial location and allow time to increase, we are effectively moving "to the left" along the function (or rather, it is moving to the right and we are stationary). Reversing the sign gives A₀ cos(kx + ωt), which is the equation of a wave propagating in the negative x direction. Note that the function A(t,x) is the fundamental solution of the (one-dimensional) "wave equation"
 
 

" 

以上は本文のほうで検討したが、あとで二つの式をもう少し検討してみるが、次の本題の一つ Phase Velocity の解説を見てからにする。

”
Since ω is the number of radians of the wave that pass a given location per unit time, and 1/k is the spatial length of the wave per radian, it follows that ω/k = v is the speed at which the shape of the wave is moving, i.e., the speed at which any fixed phase of the cycle is displaced. Consequently this is called the phase velocity of the wave, denoted by v_p. In terms of the cyclical frequency and wavelength we have v_p = λν

it follows that ω/k = v is the speed at which the shape of the wave is moving, i.e., the speed at which any fixed phase of the cycle is displaced. Consequently this is called the phase velocity of the wave, denoted by v_p. 式は簡単で

ω/k = v（velocity）

上で検討した ω と k を使うと

ω =   2πf （f = 周波数）

つまりは ω は１秒間に何回 2π するか（何周するか）を示す。

1/k は λ = 2π/k から

 　　　　　　λ
1/k  ＝　－－
　　　　　 2π

 　　　　　　　　　　λ
ω/k =　2πf　ｘ　－－  
　　　　　　　　　 2π 　　
　　＝　f　ｘ　λ

 　 ＝　(number1 / sec )   ｘ　wave length (number2 in meter)

      =   number1 ｘ　number2　in meter / sec

 　　　　　　　　　λ
ω/k =　2πf　ｘ　－－  
　　　　　　　　　 2π　　
　　
＝　f　ｘ　λ

 　　＝　(number1 / sec )   ｘ　wave length (number2 in meter)

      =   number1 ｘ　number2　in meter / sec

 したがって 単位は meter / sec で速度になる。何の速度かというと

number1 は周波数の数（数だけで＜１秒当たりはない＞）、number2 は λ で波長の数だけ＝波の１周期の長さの数（数だけで meter はない＞。ややこしい言い方だが単位を含めて考えれば
＜周波数 ｘ 波長＞で＜１波長の速度＞＜１波長が移動する速度＞ということになる。波長は物理的に実際にある長さだ。時間の方も物理的に実際にあるようなので＜１波長の速度＞も物理的に実際にあるようだ。だが周波数は＜１秒間に何回転＞、また上下運動の場合は＜１秒間に幾度上下をくりかえす＞ということなので、あくまで数に過ぎないが＜１秒あたり＞Key になる。この＜１秒あたりの数＞に＜実際に長さのある波長の長さ＞を掛けると phase velocity  というものになる。
具体的には、例えば波長1m、 角周波数ω＝2πラジアン/秒（ω  = 1）とすると

phase velocity  は 1(/sec) x 1m = 1m/sec になる。波長0.1m、角周波数ω  = 20とすると

 20(/sec) x 0.1m = 2m/sec になる。
 
波長は0.1mと短いが1秒間に20回現れるのでトータルは2mになる。だがphase velocity  はこのトータル2mの距離のことを言っているのではなく、初めの0.1mの波長がが1秒後にどこにあるかを言っているのであり、答えは20個分（数え方によっては19個分）先（前）に）にあるので0.1mｘ20/sec＝2m/secということになる。

このω と とk は "wave equation"

 
  

 に定数となって出てくるが、ω / kの逆でしかも2乗になっていて意味ありげだ。
 


"
If we imagine the wave profile as a solid rigid entity sliding to the right, then obviously the phase velocity is the ordinary speed with which the actual physical parts are moving. However, we could also imagine the quantity "A" as the position along a transverse space axis, and a sequence of tiny massive particles along the x axis, each oscillating vertically in accord with A₀ cos(kx - ωt). In this case the wave pattern propagates to the right with phase velocity v_p, as before, and yet no material particle has any lateral motion at all. This illustrates that the phase of a traveling wave form may or may not correspond to a particular physical entity.

” 

ここは波の現象の特徴の説明で言葉である程度わかるが、証明（verification）つきとなると数式

A₀ cos(kx - ωt) 
を使った説明が必要だ。 
 
１）時間を止めた場合。変数 t が定となるのでTで置き換えると

A(T,x) = A₀ cos(kx - ωT)

 　　　　2π　
k　＝　－－
　　　　　λ なので
 　　　　
 　　　　　2πx
kx　＝　－－－
　　　　　　λ で単位はradianになる。ωTの単位もradianになる。 
   　　　　　
一方
 
  

のほうは時間が止まっているということで t の微分部分は＜ゼロ＞になる。



２）xを固定した場合。変数 x が定となるのでXで置き換えると

A(t,X) = A₀ cos(kX - ωｔ)

 cos の中の単位は上とかわらずradianになる。 

 
  

のほうはxが止まっているということで x による微分部分が ＜ゼロ＞になる。 k / ω の２乗部分は

 
 　　　　　2π　　　　1　　
k/ω  =　－－  ｘ　－－
　　　　　　λ 　　　2πf　

　　　　　　1
　　　＝　－－
　　　　　　λ f　　　　
 
　　　　　　　　sec
で単位は　－－－ で速度の逆数になる。そしてこの2乗というわけだ。時間微分を2回するので
 　　　　　　　　m

つじつまはあうことになる。

　　　　　　

ｓｐｔｔ